Sekitar tahun 2010, sebuah permainan mudah alih (permua) di telefon bimbit diperkenalkan dan mendapat perhatian umum; Angry Birds. Ya, saya yakin, lebih 80% daripada pembaca pernah sekurang-kurangnya mencuba permua tersebut sekali. Di sebalik keseronokan pemain untuk menghapuskan khinzir-khinzir hijau yang bersembunyi di sebalik blok-blok kayu, sedarkah kita bahawa pembangun permua tersebut tidak mengabaikan konsep fizik semasa menghasilkannya?
Bagi entri kali ini, kita akan memasuki mode nerda dan menganalisis fizik, secara khususnya dari aspek mekanik klasik, di sebalik Angry Birds.
Kita bahagikan proses menyerang si khinzir kepada tiga komponen iaitu: 1) semasa pelancaran, 2) semasa penerbangan di udara, dan 3) semasa pelanggaran dengan khinzir atau blok kayu. Dua komponen terawal adalah apa yang dikenali sebagai analisis gerakan projektil (projectile motion).
Semasa burung merah ini dilaraskan pada lastik, kita sebagai pemain mengawal dua perkara iaitu sudut pelancaran dan panjang tarikan getah lastik (yang merujuk kepada daya yang dibekalkan). Keelastikan getah tidak diketahui dan tidak dapat diagak hanya dengan melihat pada skrin, maka daya pelancaran tidak boleh dikira; apa yang tinggal hanyalah sudut dan halaju awal burung semasa dilancarkan. Bagi permua dua dimensi sebegini, dua komponen perlu diambil kira iaitu komponen x (arah ke kiri dan ke kanan) dan komponen y (arah ke atas dan ke bawah). Katakan nilai-nilai tersebut diketahui, makan pengiraan berikut boleh dilaksanakan.
Melalui contoh ini, kita ambil halaju awal, Vo = 20 m/s dan sudut pelancaran, θ = 30°. Halaju ini perlu dileraikan kepada dua komponen, x dan y, menggunakan konsep mudah Pythagoras dan trigonometri asas seperti yang ditunjukkan. Maka, Vox dan Voy boleh dicari.
Seterusnya, setelah burung dilancarkan dan terbang di udara, pengiraan seperti berikut perlu dilakukan bagi mendapatkan jarak melintang (horizontal distance) yang dicapai oleh si burung dan adakah ia mencapai si khinzir.
Dalam mekanik klasik, terdapat empat persamaan kinematik (kinematic equations) asas yang begitu berguna:
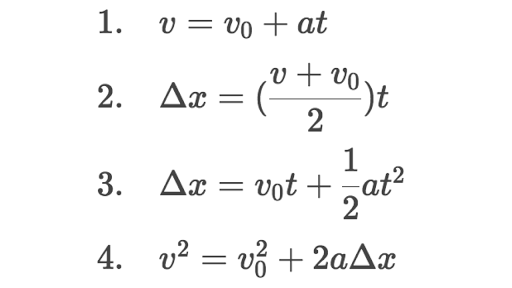Bagi analisis burung terbang dalam permua ini, persamaan ketiga diperlukan. Nilai-nilai seperti pecutan graviti (gravitational acceleration), g = 9.81 m/sˆ2 adalah diketahui sekiranya mereka tinggal di Bumi, dan katakan juga sambil bermain permainan ini, anda memegang sebuah jam randik bagi mengira masa penerbangan (time of flight) burung, dan kita ambil masa, t = 3 s. Masa bagi kedua-dua komponen adalah sama, maka t = tx = ty. Bagi komponen x, tiada pecutan yang berlaku kerana tiada daya yang menolak burung ke kanan/melintang, maka ax = 0. Oleh itu, jarak melintang, x dikira dan mendapati x = 51.96 m. Manakala, komponen y mempunyai pecutan kerana Bumi (atau apa jua planet yang mereka diami) mengenakan daya graviti menegak ke bawah dengan pecutan 9.81 m/sˆ2, maka ia adalah nilai ay. Jadi, y = -14.145 m. Ini bermaksud, si burung akan mendarat pada 14.145 m di bawah ketinggian awal semasa pelancaran.
Jika si burung berjaya mengena pada khinzir, kita perlu mengira sama ada momentum burung terdaya untuk membunuh khinzir atau memusnahkan blok kayu. Momentum adalah unit fizikal yang mengambil kira jisim objek dan halaju pergerakan. Katakan, kita ambil jisim burung, m = 1 kg. Halaju burung semasa pelanggaran boleh dikira dengan mengira halaju akhir pada komponen x dan y, dan mencari halaju paduan.
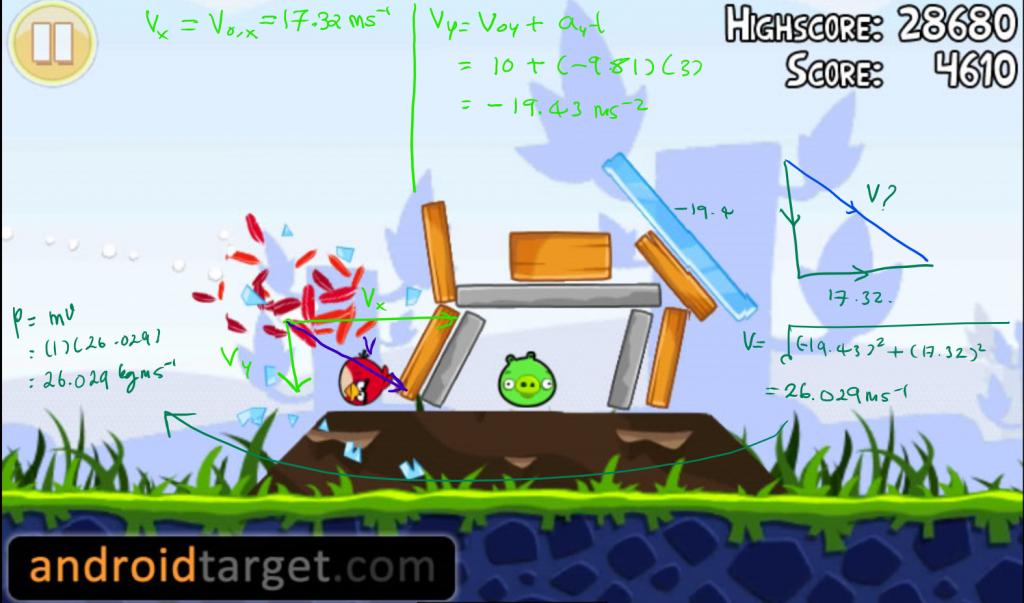
bagi komponen x, halaju akhir adalah sama dengan halaju awal Vx = Vox = 17.32 m/s kerana seperti yang disebutkan tadi, tiada daya yang dikenakan dan boleh mengubah halaju burung pada komponen x. Manakala, untuk mengira halaju akhir pada komponen y, persamaan kinematik pertama digunakan dan mendapati bahawa Vy = -19.43 m/s. Sekali lagi, menggunakan Pythagoras, kita perlu mengira hypotenuse segitiga (di bahagian kanan gambar) bagi mencari halaju paduan (resultant velocity) iaitu halaju sebenar semasa hentaman berlaku. Berdasarkan pengiraan, V = 26.029 m/s. Kemudian, dengan mudah momentum, p boleh dikira dengan menggunakan rumus p = mV = (1 kg)(26.029 m/s) = 26.029 kg m/s. Fizikawan biasanya menggunakan tekanan (pressure) untuk mengira kemusnahan yang diakibatkan oleh sesuatu pelanggaran dan untuk mengiranya, kita memerlukan masa impak (time of impact) yang bergantung kepada kelembutan si burung/khinzir/blok kayu dan turut memerlukan luas permukaan yang bersentuhan antara burung dengan objek/makhluk yang dihentamnya. Maka, bagi tidak memualkan kalian, kita berhenti pada momentum untuk memberi gambaran konseptual bagi menganalisis permasalahan ini.
Saya tidak pasti sama ada momentum sebesar ≈ 26 kg m/s adalah cukup besar untuk membunuh seekor khinzir kerana saya bukan pakar pembunuh-khinzir-menggunakan-burung (?), maka saya tidak dapat mencari kesimpulan akhir kepada proses ini, tetapi sekurang-kurangnya kita dapat belajar sesuatu, bukan?
Maka, selepas ini, jika anda bermain sebarang permua, sama ada Flappy Bird, Cut The Rope, Where’s My Water dan lain-lain yang menggunakan konsep fizik sebagai asasnya, apa kata ambil masa untuk menganalisis, untuk menambah keseronokan (atau kemuraman)!
Ayuh bermain dan meneroka dunia!
p/s: Bercakap mengenai dunia, saya mempunyai hipotesis bahawa komuniti Angry Birds tidak tinggal di Bumi kerana berdasarkan pemerhatian kasar, kadar jatuhan si burung ke darat terlalu perlahan berbanding apa yang kita alami di Bumi. Mungkin.
